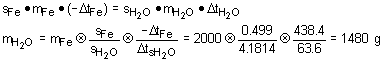| Chemistry 211-Exam 2 | Name: |
| October 24, 1997 | please print |
Instructions: Read the whole examination before starting to work on individual problems. Some problems are easier than others; work those first. Budget your time to insure that you finish the examination. Don’t waste time on problems that you find hard to finish until you have worked the others.
Part I Answers:
1. a |
6. d |
11. d |
16. d |
2. d |
7. a |
12. a |
|
3. b |
8. b |
13. b |
|
4. d |
9. a |
14. b |
|
5. c |
10. b |
15. d |
Part II: Solutions
1. The mass of a grain of salt was 0.01000 g. What would be the mass of one mole grains of salt if they all weighed the same?
a. 6.02x1021 g |
c. 6.02x1025 g |
b. 1.66x10- 26 g |
d. 100 g |
Solution:
Mass of 1 mol = mass of one particle times number of particles.
![]()
2 What is the mass of chlorine in 15.55 g of NaCl?
a. 5.57 g |
c. 35.45 g |
b. 3.86 g |
d. 9.43 g |
Solution:
Use weight fraction to determine mass of Cl:
![]()
3. What would be the volume of 0.250 mol of an ideal gas if 0.500 mol of another ideal gas occupied a volume of 55.7 L at the same pressure and temperature?
a. 55.7 L |
c. 111.4 L |
b. 27.8 L |
d. not enough information given. |
Solution:
When dealing with an ideal gas; the volume is related to the number of moles and doesn’t depend upon which gas that you are using.
![]()
4. What volume of 0.100 M NaOH can be produced from 200.0 mL of 6.25 M NaOH.
a. 3.20 L |
c. 3.20 mL |
b. 12.5 mL |
d. 12.5 L |
Solution:
This is a simple dilution problem.
![]()
5. What is the molarity of NaOH in a solution made by dissolving 12.5 g of NaOH in 100.0 mL.
a. 0.00313 M |
c. 3.13 M |
b. 0.00800 M |
d. 0.800 M |
Solution:
Determine moles of NaOH and then use the definition of molarity.
![]()
6. The vapor pressures of O2 and N2 in a gaseous mixture were 255 mmHg and 50 mmHg; the mole fraction of oxygen in the mixtures was
a. 0.164 |
c. 83.6% |
b. 16.4% |
d. 0.836 |
Solution:
Use the definition of mole fraction:
![]()
7. Under what set of conditions does CO(g) best follow the ideal gas law?
a. high temperature and low pressure |
c. high temperature and high pressure |
b. low temperature and high pressure |
d. standard temperature and pressure |
Solution:
Remember that we want conditions where the molecule will not interact with other molecules; this is less likely to occur when the pressure is low and the temperature is high!
8. When two solutions containing different compounds were mixed, the solution became warm. This means that
a. no reaction occurred |
c. an endothermic reaction occurred. |
b. an exothermic reaction occurred |
d. a reaction occurred; there was no energy change. |
Solution:
The solution warms up; this means that the reaction supplied heat to the solution. The reaction must be exothermic.
9. Determine the mass of precipitate that would form if 50.00 mL of 0.1000 M Cu(NO3)2 reacted with 50.00 mL of 0.1000 M NaOH.
a. 0.2439 g |
c. 0.4028 g |
b. 0.4877 g |
d. 0.2014 g |
Solution:
Recall that all nitrates are soluble as are all sodium compounds; this leaves only Cu(OH)2 as the precipitate. Determine which reagent is limiting; use it to determine the mass of product. Balanced net ionic equation is
![]()
Since there is the same amount of both reagents and since 2 hydroixdes are consumed for every metal ion, the hydroxide is the limiting reagent and will produce the smallest amount of product. We use it to determine the mass of precipitate.
![]()
10. Determine the molarity of a solution of potassium dichromate, if it took 50.00mL of 0.1000 M NaCl to completely react with 50.00 mL of the dichromate solution.
![]()
a. 0.1000 M |
c. 0.6000 M |
b. 0.01667M |
d. 0.3000 M |
Solution:
This is a stoichiometry problem. Simply use stoichiometry to determine the molarity of the dichromate (d) from the given molarity of choride (c). Don’t forget to include stoichiometric coefficients!
![]()
11. Combustion analysis of a compound containing only C and H gave 0.04977 g of CO2 and 0.02444 g of H2O. Mass spectrometric analysis reavealed a molecular mass of 72.00 g/mol. The number of hydrogens in the compound is
a. 8 |
c. 10 |
b. 6 |
d. 12 |
Solution:
This was a simple molecular problem, but had non-integer co-efficient which made it harder. Since we were given the molecular mass, I felt that the easiest way was to determine the mass % of hydrogen and then to find out the mass of hydrogen in one compound and then to calculate the moles of hydrogen in one mole of the compound.
| mass fraction of hydrogen, fH: | 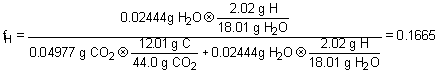 |
moles H/mol of compound: |
|
12. The density of a particular gas as 298 K was 0.0588 g/L, What would its density be at 100K (assuming it does not condense at this temperature)?
a. 0.175 g/L |
c. 0.0148 g/L |
b. 0.234 g/L |
d. 0.0197 g/L |
Solution:
Using the ideal gas law we determined a relationship between density and other quantities; this equation shows an inverse relationship between density and temperature! Thus a lower temperature should mean a higher density.(i.e. only answers a and b make any sense.
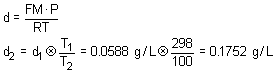
13. A reaction evolved CO which was collected over water at 20.0°C. What is the mass of CO collected if the volume was 500.0 mL at 755.5 mmHg and the vapor pressure of water at this temperature is 17.5 mmHg?
a. 0.0202 g |
c. 0.971 g |
b. 0.565 g |
d. 1.77 g |
Solution:
Use ideal gas law subtracting pressure from water first!
Pressure of CO: |
|
mass of CO: |
|
14. A gas was initially at a pressure, volume and temperature of 1.00 atm, 0.1000 L, 25.0°C ,respectively. It was expanded so that the pressure decreased by a factor of 3.55 and the volume increased by a factor of 1.35. What was the final temperature?
a. 9.50°C |
c. 784 K |
b. 113 K |
d. 339 K |
Solution:
This is the ideal gas also; we don’t really need to know the initial pressure and volume to solve this problem.
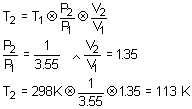
15. The RMS speed of O2 molecules at 21°C was 479 m/s. At what temperature would the molecules have to be to have a speed of 50.0 m/s.
a. 2.19 K |
c. 30.7 K |
b. 201 K |
d. 3.20 K |
Solution:
Recall the equation for the rms speed of a molecule; we see that the molecular speed is proportional to the square root of temperature. This leads us to the form of the equation that allows us to solve the problem.
![]()
16. A blacksmith dropped a 2.00 kg piece of steel (iron, sFe = 0.449 J/g× °C) into water, which was initially at 25.0°C, and waited until the steel temperature was the same as the final temperature of water (88.6°C). Determine the mass of water (the heat capacity of water is 4.1814 J/g× °C) if the initial temperature of the metal was 800.0K.
a. 2.43 kg |
c. 2620 g |
b. 544 g |
d. 1.48 kg |
Solution:
The heat lost from steel is transferred to the water. Set the two equations equal to each other and then substitute in known values.