Some population ecology...
(There are quite a few equations in here - they look much better with the pdf version).
We're back to following the text for a while. What follows starts with chapter 5. This
will probably take us a while since this (and the next few chapters) are very "dense",
meaning a lot of material is presented in very few pages. (I did warn you we'd be doing
math for two or three weeks!).
Life tables.
Life tables are a nice way to get a snapshot of populations. They can provide information
on age distribution, growth, mortality, survival, etc.
Since most of you should have had this in ecology, let's start right in with the example
from the text (Himalayan thar introduced into New Zealand - note that this is sometimes
called a "static" life table since it takes a snapshot of the population - it doesn't follow
every individual from birth to death).
Table 5.1, page 148. Unfortunately, the authors introduce an annoying rounding
error. A slightly revised version is given below:
Age (x) Fx fx lx dx qx px mx mx x Fx
0 205 1 0.5317 0.5317 0.4683 0 0
1 94 96 0.4683 0.0098 0.0208 0.9792 0.005 0.47
2 97 94 0.4585 0.0244 0.0532 0.9468 0.135 13.095
3 107 89 0.4341 0.0488 0.1124 0.8876 0.44 47.08
4 68 79 0.3854 0.0537 0.1392 0.8608 0.42 28.56
5 70 68 0.3317 0.0634 0.1912 0.8088 0.465 32.55
6 47 55 0.2683 0.0585 0.2182 0.7818 0.425 19.975
7 37 43 0.2098 0.0537 0.2558 0.7442 0.46 17.02
8 35 32 0.1561 0.0488 0.3125 0.6875 0.486 17.01
9 24 22 0.1073 0.0341 0.3182 0.6818 0.5 12
10 16 15 0.0732 0.0244 0.3333 0.6667 0.5 8
11 11 10 0.0488 0.0195 0.4 0.6 0.411 4.521
12 6 6 0.0293 0.411 2.466
>12 11 0.411 4.521
207.268
- Column 1 - (x) simply the age (in this case going from 0 to >12)
- Column 2 - (Fx) number of individuals found in each age group.
- Column 3 - (fx) a modification of column 2. We'll use it instead of column 2
to generate the rest of the table. We'll explain how this was
generated below. For now it's a "smoothed" version of Fx.
- Column 4 - (lx) survivorship. This is the proportion of individuals that
survived into the present age. Since we started with 205
individuals at age 0, for age 1 survivorship would be 96/205 =
.4683, at age 2, it would be 94/205 = .4585, etc.
- Column 5 - (dx) mortality. The proportion in each age group that does not
make it into the next age group. Thus, (205-96)/205 = .5317, and
this is the proportion of individuals that die at age 0. At age 1, we
have 96-94)/205 = .0098 (an easier way - and the usual way - to do
this is simply to use lx - lx+1, so for example, at age 1 we have l1 =
.4683, l2 = .4585, so we have .4683 - .4585 = .0098) .
- Column 6 - (qx) mortality rate. The proportion at each age interval that doesn't
survive to the next age interval. For example at age 1 we have 96
individuals alive. At age 2, we have 94. 2 individuals died. Thus
the proportion of individuals that died is 2/96 = .0208 (or we could
use dx/lx to get the same thing.
- Column 7 - (px) survival rate. Simply 1 - column 6 (the proportion surviving
into the next interval).
Some notes on the mysterious column 3:
Note that it doesn't make sense to talk about proportions larger than one,
or similar anomalies.
- raw counts of different age groups will sometimes lead to such
anomalies as more individuals alive at age 4 than at age 3. Note
that this is obviously possible (e.g. in a declining population).
To avoid this and make sense out of it all, a smooth is applied. The
authors use regular least square regression to smooth out the data. To see
this, let's look at the following graph:
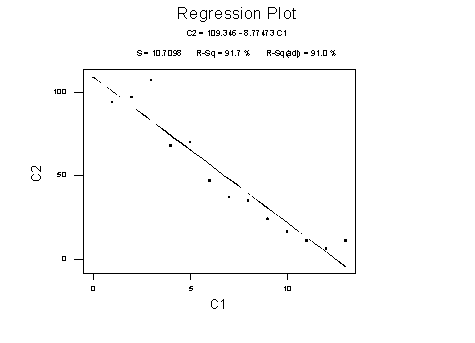
Unfortunately, various diagnostics indicate that the regression is not doing
a particularly good job (residuals have a curve and funnel - about as bad as
things can get). To get a better fit, we transform the variables.
Without going into too many details, a standard thing to do to deal
with a funnel is to take a log transform of the y-variable, but in this
case more needed to be done, so the authors also included a
quadratic term for the x variable (this often gets rid of the curve -
in statistical terms, their residual plot didn't look good until they
did this all this).
We're skipping over a LOT of statistical details here, but it's not a
class in statistics. Incidentally, introductory classes usually don't
cover log transforms or quadratic terms.
If you find yourself in a position were you need to do
something like this, make sure you talk to a statistician or
take a good regression class.
Note that although we're not trying to get p-values here, we are
trying to do a good job estimating numbers. A regression analysis
will do that for us, and if we're doing that, it probably makes sense
to pay attention to the necessary procedures, requirements and
assumptions of a regression analysis.
Anyway, the authors wind up with the following (presumably due to
rounding errors, it seems impossible to replicate the exact results):

So to get the numbers in the second column, they simply plug in Fx for x.
For example, for age 3 we get:

solving this gets we get log10 y = 1.94786, and exponentiating this
to get our original y, we get y = 88.687 (the table rounds this off to
89, since ".687" himalayan thar are kind of silly).
Comment # 1: trying to replicate this gives:

Comment # 2: statisticians usually use natural logs!
Comment # 3: Don't round anything until you're ready to print the results.
Comment # 4: It comes out a little closer to the text if we just drop the >12
age category instead of substituting "13" as I did, but the rounding error
doesn't go away.
Important: the number for age = 0 was not derived from the regression
equation. There are two good reasons for this:
- we don't know what's happening outside the range of our
analysis (we have no data at age 0, so how can we know what's
going on there)?
- we can get a better estimate using a fecundity table (more
shortly).
Let's skip of table 5.2 for the moment and look at fecundity (the last two columns
in the table above)
- mx is the proportion of females giving birth to a daughter during age x.
We usually get this information from field data. If we know the
proportion of females giving birth at each age category, we can use this to
estimate the number of births (simply multiply mx x Fx (or fx)) at a given
time. The last column above gives this figure, and then sums this. This is
the number we put in the row for age 0 in the fx column (the usual
rounding error is present).
- females & daughters are used, since that gives the "per capita"
increase (if sons were included, the growth rate would be too high).
Since it's per capita, when we multiply this by the total number of
individuals, it all works out.
Rate of increase:
Before we figure out table 5.2, we need to understand this.
Over a year (or reproductive cycle), the increase (or decrease) in a population can
be estimated as Nt+1/Nt, where N is population size and t = time step (e.g. year).
This is sometimes given as (lambda) and sometimes as R (depends on the text).
But often, instead of either of these, we like to use r, which is given as follows:

Where ln is "natural log", not log10. We can estimate r either as above, or if
several years of data are available, we can use a regression and estimate the slope
of ln(N) on t.
r is positive if a population is growing, negative if it's decreasing, and 0 if it's
stable. Not also that it's symmetric: if r = .69, the population is doubling, if
r = -.69, then it is halving.
Incidentally, if we try to use life tables to derive r, we could try to use the
following equation:

this would give an exact number for r (assuming our life tables are
accurate), but is difficult to solve without computer iteration.
Note: this whole subject can get quite complicated quickly, but this is not an
ecology class as such, we're just trying to refresh our memories a bit when it
comes to life tables. We'll be using this a little later to analyze populations.
Stable age distribution:
We also need to be aware that even if the age distribution is stable for a long time,
that does not mean the population is not increasing or decreasing.
- e.g., lx might stay very constant, but this doesn't indicate raw numbers.
We use the concept of "stable age distribution" to indicate this. It's defined as by:

- note that Sx is essentially the proportion of the population at age x, but
only if lx and mx have remained stable for a some time. The definition as
given assumes this (note also that r depends on lx and mx).
Table 5.2:
Now we're ready to look at this one. It incorporates information on population
increase (the authors just "give" this) to adjust population figures. Note that there
are two things going on here:
1) the fx column now indicates the population after "growth". If you add
up the Fx and fx columns you get two different numbers (in the previous
example, these are the same except for rounding error).
2) The main reason for doing this is to get a better fit (if you thought the
statistics for the first example were bad, this one's much worse). The main
objective here was to get good numbers for lx, dx, etc.
Essentially, fx had to be adjusted in a more complicated way to
allow for the rate of increase. Each value of Fx was multiplied by
erx (where r = .12). The resulting numbers were then smoothed
using a probit function (a probit function is a way to do non-linear
regression).
Looking just at the Fx column, superficially it appears that a regular
linear regression should gives nice smooth data (it gives nice
residuals), but since the author was worried about changing age
structures (i.e., the regression equation would become invalid
quickly) and comparing several different populations he used this
rather more complicated approach.
Briefly, here are the details on table 5.2:
Age (x) Fx fx lx dx qx px
0 43 1 0.3721 0.3721 0.6279
1 25 27 0.6279 0.0233 0.037 0.963
2 18 26 0.6047 0.0233 0.0385 0.9615
3 18 25 0.5814 0.0465 0.08 0.92
4 19 23 0.5349 0.0233 0.0435 0.9565
5 11 22 0.5116 0.0698 0.1364 0.8636
6 12 19 0.4419 0.0465 0.1053 0.8947
7 8 17 0.3953 0.0698 0.1765 0.8235
8 2 14 0.3256 0.0698 0.2143 0.7857
9 3 11 0.2558 0.0465 0.1818 0.8182
10 4 9 0.2093
>10 5
Birth and death rates:
There are several ways of looking at this, but we'll stick with the text.
B - birth rate. This is the number born/population size (other than newborn). We
can calculate it either from field data or from our tables as follows:

eb - finite birth rate. Similar to B, but now we ignore death rates, so we get this
number by simply by calculating the population size immediately after birth by the
population size immediately before birth. It can also be calculated from our tables
by:

We can relate B and b (see text, but some simple manipulations of the above
should make it obvious)
D - death rate. This (and e-d) are defined similarly to the above. D is the
proportion of the population that dies over a year:

with the needed quantities gotten from the life tables.
e-d - this is defined as the population size at the end of a time unit (but prior to
births), divided by the population at the beginning of the time unit. An easy way
to get this is simply e-d = 1-D.
and d, of course, would be ln(1-D).
(The text states r = b-d, but note that r is in the definition of D, so this is not an
easy way to get r).
Some comments on all the above:
We're not done yet, though this should be the worst bit.
The authors don't really differentiate between cohort life tables and static life
tables. A cohort life table is one in which a population is followed throughout it's
entire life cycle (usually difficult to do with larger animals). A static life table
takes a "snapshot" of current conditions.
Often the upshot of a lot of this is to get an estimate for r. This can be derived in a
number of different ways - the text simply says not to use:

and instead to focus on getting two population estimates at different times.
- With the explosion in computer power, it is not unreasonable to simply
solve this iteratively (don't worry, we won't do it here!).
- There are several other ways of getting at r using life tables, though most
of these are based on estimates. They often also assume you're using a
cohort life table. See a good Ecology text for more explanations.










