Mental Math
Often it is necessary to perform complicated calculations and rely heavily on a handheld calculator to produce the correct result. We do not always know if the answer is correct. By using simple techniques it is possible to decide if the calculator is correct, i.e., that we entered the numbers correctly. Sometimes we can arrive at an answer quicker by estimation and nearly as accurately. We may not even need a calculator to perform the calculation at the accuracy level required. Mental math can save lots of valuable time. Think about the time you might save during exams.
Logarithms and Antilogarithms
We use logarithms a lot in calculations such as vapor pressures, cell potentials, activation energies and of course pH. We can determine the log of essentially any number with an accuracy that is astoundingly good (~±10%). We need to memorize the log of only one number (2) and use the principles of logs for other numbers.
Logarithms: You should realize that all numbers can be expressed on a base 10 scale.
For example the exponent for the power of ten representation of 2 would be 0.301 or 2 = 100.301 .
Similarly the exponent for 5 would be 0.699 or 5 = 100.699
When we say that we want the log of a number, we are asking for the exponent that would represent that number. In the above examples we would have:
| log 2 = 0.301 | log 5 = 0.699 |
1. If you haven't already, memorize these relationships:
| Log base ten | log (A· B) = log A + log B | log An = n log A | |
| Natural log | ln (A· B) = ln A + ln B | ln An = n ln A |
2. Memorize numbers for log range from 1 - 10, i.e., memorize the logarithms of 2, 4 and 8.
Given: log 2 = 0.301 » 0.30 Get the other two from log 2:
log 4 = log 22 = 2· log 2 = 0.60
log 8 = log 23 = 3· log 2 = 0.90.
If we are asked the log of any of these numbers, we can answer immediately. Most numbers asked would not be one of these. To obtain others we assume that a linear interpolation will be a reasonable estimation.
E.g.1 Determine the log of 3, 6, 9.
Solution:
Three is half way between 2 and 4, the log 3 should be close to ![]() . Actual is 0.48.
. Actual is 0.48.
Similarly:
![]() Actual
is 0.78
Actual
is 0.78
![]() Actual
is 0.95.
Actual
is 0.95.
E.g.2 Determine log of 30, 60, 90, 0.030, 0.060, 0.090
Solution: Express each in scientific notation, separate multiplied parts, and take logs.
log 30 = 3.0x101 = log 3.0 + log 101 = 0.45 + 1.00 = 1.45 Actual = 1.48
| Number | Estimated | Actual |
| log 60 | 1.75 | 1.78 |
| log 90 | 1.95 | 1.95 |
| log 0.030 | - 1.55 | - 1.52 |
| log 0.060 | - 1.25 | - 1.22 |
| log 0.090 | - 1.05 | - 1.05 |
Antilogarithms: These are the numbers that result when a given number is used as the exponent to a base 10.
E.g. Determine the antilogarithm of 0.301 and 0.602
Solution: antilog 0.301 = 100.301 = 2 and antilog 0.602 = 100.602 = 4.0.
We can use the strategy outlined above to determine the antilog of essentially any number with surprising accuracy. We must work in the reverse direction but the strategy is essentially the same.
E.g.2 Determine the antilogarithm of 0.2, 0.5, 0.7.
Solution:
0.2 is two thirds of the way between log 1 (= 0) and log 2 (=
0.3). A linear interpolation gives: ![]() . Actual is 1.6.
. Actual is 1.6.
0.5: is between log 2 (= 0.3) and log 4 (= 0.6); linear interpolation gives:
![]()
Actual is 3.2.
0.7 is between log 4 (= 0.6) and log 8 (= 0.9); linear interpolation gives:
![]()
Actual is 5.0.
More complicated antilog: Separate into the sum of two numbers. The first one should be a positive number between 0 and 1. The second number should be an integer. Determine antilog of each using linear interpolation. The
E.g.3 Determine the antilog of 1.4, 6.8, 3.1, - 1.4, - 6.8, - 3.1
1.4 antilog 1.4 = antilog (0.4 + 1.0) = 101.4 = 10(0.4 + 1.0) =100.4x101 ;
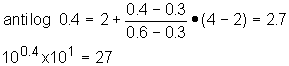
Actual is 25
6.8: antilog 6.8 = antilog (0.8 + 6.0) = 106.8= 10(0.8 + 6.0) =100.8x106 ;
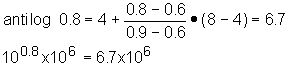
Actual is 6.3x106
3.1: antilog 3.1 = antilog (0.1 + 3.0) = 103.1= 10(0.1 + 3.0) =100.1x103 ;
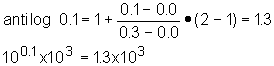
Actual is 1.3x103
- 1.4 antilog - 1.4 = antilog (0.6 + - 2.0) = 10-1.4 = 10(0.6 - 2.0) =100.6x10-2 ;
![]()
- 6.8: antilog - 6.8 = antilog (0.2 - 7.0) = 10- 6.8= 10(0.2 + - 7.0) =100.2x10-7 ;
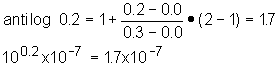
Actual is 1.6x10-7
- 3.1: antilog - 3.1 = antilog (0.9 - 4.0) = 10-3.1= 10(0.9 - 4) =100.9x10-4 ;
![]()
Actual is 8.0x10-4
Better Yet! Do you want even better precision? Try this. In addition to memorizing log 2 memorize log 3 = 0.48. Then use the same principles of logarithms to determine log and antilog of any other number. You should be able to improve your precision to ± 5% or even better.
If you have a question or suggestions, please send me an email message at jschreif@gmu.edu . Your request will be answered shortly.