Questions for Chapter 1
N5+ Cation Makes Explosive Debut --
High-energy ion is first new all-nitrogen species in 100 years.
Along with colleague William W. Wilson, Karl O. Christe has synthesized and characterized a salt containing the N5+ cation. The cation is the first new all-nitrogen species to be synthesized in isolable quantities in more than a century, and only the third ever to be produced. Prior to the new work, only molecular nitrogen, N2, isolated in 1772, and the azide ion, N3-, first synthesized in 1890, had ever been isolated. He calls the resulting white powder "marginally stable" at 22oC. With careful handling, he was able to obtain mass spectroscopic data on the compound at that temperature. However, his presentation included slides of his low-temperature laser spectroscopy apparatus "before" and "after" a sample of a few milligrams of the N5+ salt exploded and destroyed the sample chamber. C&EN Jan. 25, 1999
1. a) A similar and classic problem is to draw the resonance structures for the azide ion (N3)-, which you might want to do first.
1. b) The N5+ molecule's connectivity is N-N-N-N-N. Draw several resonance contributors for the N5+ species such that each contributor has at least three multiple bond sets (e.g. 3 double bonds, 1 triple + 2 double bonds, etc.). Include all non-bonding electron pairs. Assign formal charges to all atoms in the drawings.
Because of the symmetry of N5+, there should be an equivalent resonance contributor for each one you draw initiallly ("reading" the structure from left to right and from right to left). Be sure to state which contributors are equivalent.
[Answer 1]
2. The actual structure of the N5+ ion has an N-N-N bond angle of ~120o around the central nitrogen. From this information, which resonance structures cannot be contributors to the resonance hybrid? Remember, resonance contributors differ only in the placement of the electrons on a fixed set of nuclei -- the nuclei cannot change position and so the bond angles cannot change. (For the purpose of merely drawing resonance structures in the absence of geometry information, you don't need to consider geometry.)
[Answer 2]
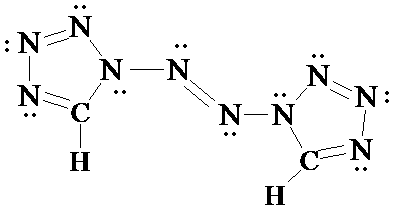
3. Here is another N-containing molecule structure. How many carbon and hydrogen atoms are present? Draw in all non-bonded electrons on the nitrogen atoms. What is the hybridization of the two central (identical) N atoms? [This is a neutral molecule and no formal charges are shown. So assign the N's non-bonded pairs using those facts.]
[Answer 3]
4. Draw all isomers with the molecular formula C2H4O2 that contain one double bond (isomers of acetic acid) but do not have a formal charge on any atom. This is a tough question, but you should make some headway with it.
[Answer 4]
Try the problems from the MIT Open Course site Problem Set 1(#1, 3, 5, 6) There are answers also.
a) Determine the total number of valence electrons for the azide N3- structure: 3x5+1=16. The molecule is linear, and so 2 covalent electron pairs are necessary to connect the three nitrogen atoms in the molecule.
With so many valence electrons and only three atoms, there are a lot of possibilities for pi bonds and non-bonding electrons. Begin with only single bonds, perhaps, but when you are finished with them all, you will recognize that these are not important contributors because better contributors have more covalent pi bonds. Also notice in each of these structures that two nitrogens lack an octet.
Put a double bond between the first two N's and then assign the remaining electrons as non-bonded pairs. Next, put the double bond betwen the last two N's and assign the remaining electrons. Recognize that you can accommodate a triple bond between two N's, also. Although you might think the 2- charge on N's in the triple-bonded species is unfavorable, notice that in these two contributors, all atoms have an octet.
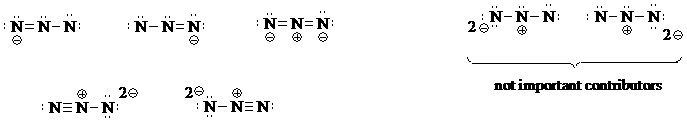
b) First determine the total number of valence electrons needed for the N5+ structure, which is 5x5-1=24.
Then determine how many electrons will have to be distributed after some of the total number are used to connect the five N's with single bonds. Draw several possibilities with varying positions of the required 3 multiple bonds, for example N=N=N=N-N. Show the remaining electron pairs. Try to work the problem systematically. Here are some possible resonance structures.
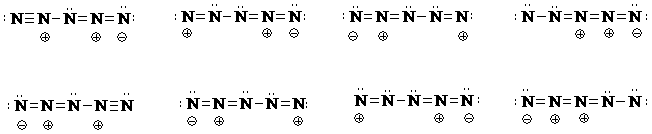
The bottom row of structures are the equivalent resonance contributors of the structures drawn directly above. (If you rotate each structure on the bottom 180 deg, in the plane of the page, you should see how each top and bottom structure is equivalent.)
Answer 2: You can answer with either VSEPR or hybrid orbital language, as follows:
A bond angle of ~120o suggests use of sp2 hybrid orbitals [three orbitals; trigonal planar geometry; ~120 deg. angles], which means the N atom could have 3 sigma bonds or 2 sigma bonds + 1 n.b. pair or 1 sigma bond + 2 n.b. pair. You can eliminate all resonance structures that don't conform to the necessary electron distribution around the central nitrogen. The first three equivalent pairs all have a central N with 2 sigma + 1 n.b. pair. The fouth pair's central N has only 2 sigma bonds and the geometry would be linear with 180 deg. bond angle.
The central N has two sigma bonds + 1 non-bonding pair, so sp2, trigonal planar, ~120 deg. angles.
Isomers of C2O2H4 that have at least one double bond in the molecule
1. The first isomer we looked at was acetic acid, CH3CO2H, which, when rewritten as an expanded structure, looks like this. It doesn't matter whether the C=O is drawn toward the top or bottom of the page, or whether the CH3 group is written on the right and the OH on the left. These merely represent rotations of the molecule in space.
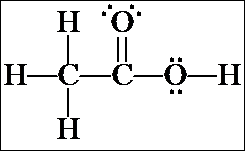Count all the valence electrons for the molecular formula and confirm that there are the same number of valence electrons shown in the structural formula (24). Also confirm that there are no formal charges on any of the atoms. [Note: resonance structure(s) may be written for the acetic acid structure, but they will have formal charges. We will not consider these now – we are looking only at the most stable resonance contributor for each isomer and none of them have formal charges.]
2. How do we start drawing additional isomers? First, decide what to do with the non-hydrogen atoms. Remember, an H will always be on the periphery of the molecule with only one bond between it and another atom so show them in a later step.
a) It is tempting to write all the C's and O's in a horizontal line and go from there. The instructions say the structure must contain one (and only one) double bond. You can start at the left and put it between the two C's.
Now draw in H's. Carbons must fill their valence of four by bonding to H's, otherwise they will carry a formal charge. The terminal O must also be bonded to H or it will have a formal charge; the internal O cannot be bonded to H or it will have a formal charge. (Confirm these statements after adding the remaining valence electrons.)
So far, 16 valence electrons are shown as bonding electrons. Add the remaining electrons as non-bonding pairs on the O's. The completed structure shown in the box is an isomer.
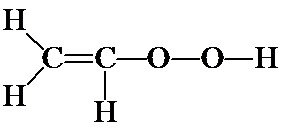
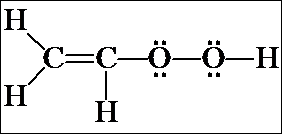
b) It is good practice to proceed systematically. In a) above, you put the double bond between the two C's. What about putting it between the C and O (i.e., C-C=O-O), or between the two O's (i.e., C-C-O=O)? You should confirm, by adding H's and non-bonding electrons that these structures will have formal charges.
c) You have now exhausted the possibilities for a continuous CCOO chain of atoms containing one double bond. Next, try a different atom order in the chain, COCO. There are three places a double bond could go: between a terminal CO, the internal OC, or the terminal OC. Only the last choice will ultimately yield a structure without formal charges (confirm this at the end of this section).
Put hydrogens on the structure so there are four bonds to each C (this uses all the H's). And then assign the remaining valence electrons to the oxygens. This is another valid isomer.
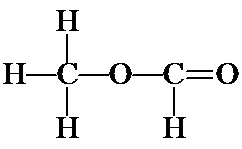
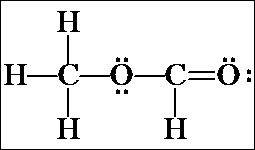
d) Another possibility for a continuous chain is OCCO. Follow the same steps as above, to yield the following structures:
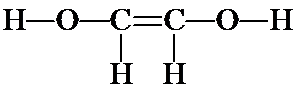
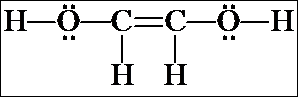
The isomer in the box actually exists as two "geometric isomers" and so counts as TWO more isomers. We will not examine geometric isomerism until the next chapter.
The double bond can also be between either CO to yield the following structures:
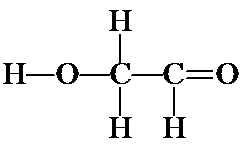
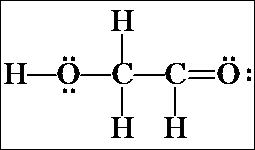
e) The last possibility for two C's and two O's in a continuous chain is a C-O-O-C. Confirm that this connectivity results in structures with formal charges.
As you look back at the acetic acid isomer at top, notice the C and O atoms are not in a continuous chain, but rather a doubly-bonded O branches off the middle of a CCO chain. Or described differently, two O's and a C are bonded to a central C; one of the O's is doubly-bonded (the O's are equivalent and it doesn't matter which is doubly-bonded). A structural variation is to put the double bond between the two C's, as shown below.
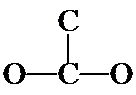
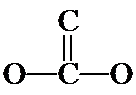
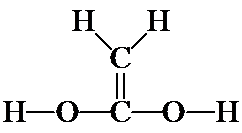
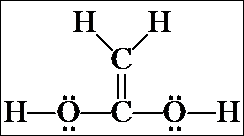
3. These are the seven isomers of C2O2H4 that contain a double bond. (There are four more that contain the non-hydrogen atoms in a cycle and no double bond.) Even though you probably could not do it on your own at first, from beginning to end, you should understand how the problem was approached and how you can follow this same process on slightly simpler systems.
4. As the last exercise involving these isomers, you should choose each C and O in each structure and state what the geometry is around each atom according to VSEPR.